二分 + 2-SAT + cdq优化建图

首先看到 $k$ 的限制， $k$ 越大越不可能合法，可以二分。

然后考虑一个划分中一个数非 $a$ 即 $b$ ，可以用 2-SAT 判定。

然后发现连边稍微有点多，但是连边的时候可以一下子连某个区间，考虑可以数据结构优化一下。

再细看一下，前两个条件都是偏序的形式，所以想到 cdq 分治。

第一维按原数组顺序即可，分治下去，用归并的方式可以将第二维排序。然后每次处理从右区间连向左区间的边。

可以发现，右区间对左区间的限制条件是一个前缀或后缀，可以考虑直接连出一条链然后把条件从链中间插进去。

假设当前分治区间 $[L,R]$ 。

对于左区间 $[L,mid]$ 的那条链可以这样建：

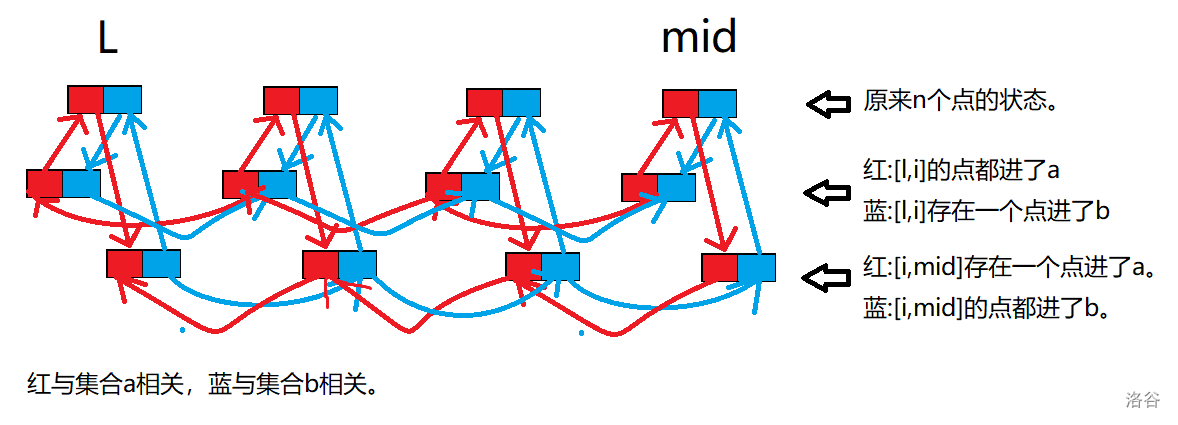
那么可以发现，对于形如“若 $i$ 进了 $a$ (或 $b$ )，则某个前缀中的点都进了 $b$ (或 $a$ )。” 的条件都有唯一对应的点。所以直接双指针找到对应点，模拟条件把区间 $[mid+1,R]$ 的点往链上面连边就可以了。在代码中有详细说明。

然后直接跑 tarjan 判定 2-SAT 即可。

值得一提，跑完 tarjan 可以只用判定原先的点及对立点是否在同一个强连通分量中即可，因为 cdq 分治附加上的点与原先的点直接相关，不可能在原先的点符合条件的基础上这些点上出现矛盾。

不难发现，连出来的边是 $O(n\log n)$ 的。因此总复杂度 $O(n\log n\log V)$ 。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include<cstdio>
#include<cstring>
#define rep(a,b,c) for(int c(a);c<=(b);++c)
#define drep(a,b,c) for(int c(a);c>=(b);--c)
#define grep(b,c) for(int c(head[b]);c;c=nxt[c])
typedef long long LL;
inline int read()
{
	int res=0;char ch=getchar();while(ch<'0'||ch>'9')ch=getchar();
	while(ch<='9'&&ch>='0')res=res*10+(ch^48),ch=getchar();return res;
}
template<typename T> inline T min(const T &x,const T &y){return x<y?x:y;}
const int N=2e4+10;int a[N],n,I[1000010]; struct Nd
{
	int p,v;inline Nd(const int &x=0,const int &y=0){p=x;v=y;}
	inline bool operator<(const Nd&x)const{return v==x.v?p<x.p:v<x.v;}
}w[N],t[N];
namespace TwoSat
{
	const int N=1e6+10,M=5e6+10;
	int head[N],des[M],nxt[M],cgt,S=1,low[N],dfn[N],tot,stk[N],top,cdt,h2[N],scc[N];bool iss[N];
	inline void ins(const int &x,const int &y){nxt[++cgt]=head[x];des[head[x]=cgt]=y;}
	inline void tarjan(const int &u)
	{
		iss[stk[++top]=u]=true;low[u]=dfn[u]=++cdt; grep(u,i)
		{
			int v=des[i];if(!dfn[v])tarjan(v),low[u]=min(low[u],low[v]);
			else if(iss[v])low[u]=min(low[u],low[v]);
		}
		if(dfn[u]==low[u]){int v;++tot;do iss[v=stk[top--]]=false,scc[v]=tot;while(u!=v);}
	}
	inline bool Judge()
	{
		cdt=tot=0;memset(dfn,0,(S+2)<<2);memset(scc,0,(S+2)<<2);
		rep(1,S,i)if(!dfn[i])tarjan(i);
//		rep(1,n,i)printf("(%d,%d) ",scc[i],scc[i+n]);puts("");printf("QAQAQ :: %d\n",tot);
		rep(1,n,i)if(scc[i]==scc[i+n])return false;
//		for(int i=n<<1|1;i<=S;i+=2)if(scc[i]==scc[i+1])return false;
		return true;
	}
}
using TwoSat::head;using TwoSat::cgt;using TwoSat::Judge;using TwoSat::ins;using TwoSat::h2;using TwoSat::S;
int idx[N][2],K;inline void cdq(const int &l,const int &r)
{
	//idx[i][0]   --> [i,r] all in a
	//idx[i][0]+1 --> [i,r] not all in a
	//idx[i][1]   --> [l,i] all in b
	//idx[i][1]+1 --> [l,i] not all in b
	if(l==r)return;const int &mid=(l+r)>>1;cdq(l,mid);cdq(mid+1,r);
	rep(l,mid,i)
	{
		ins(idx[i][0]=++S,w[i].p);ins(w[i].p+n,++S);
		ins(idx[i][1]=++S,w[i].p+n);ins(w[i].p,++S);
	}
	rep(l+1,mid,i)
	{
		ins(idx[i-1][0],idx[i][0]);ins(idx[i][0]+1,idx[i-1][0]+1);
		ins(idx[i][1],idx[i-1][1]);ins(idx[i-1][1]+1,idx[i][1]+1);
		//if()
	}
	int j=l-1;rep(mid+1,r,i)
	{
		while(j<mid&&w[j+1].v<=w[i].v-K)++j;
		if(j!=l-1)ins(w[i].p,idx[j][1]),ins(idx[j][1]+1,w[i].p+n);
		//if(w[i].p in a) [l,loc(w[i].v-K)] all in b
		//if([l,loc(w[i].v-K)] not all in b) w[i].p in b
	}
	j=mid+1;drep(r,mid+1,i)
	{
		while(j>l &&w[j-1].v>=w[i].v+K)--j;
		if(j!=mid+1)ins(w[i].p+n,idx[j][0]),ins(idx[j][0]+1,w[i].p);
		//if(w[i].p in b) [loc(w[i].v+K),r] all in a
		//if([loc(w[i].v+K),r] not all in b) w[i].p in a
	}
	int pl=l,pr=mid+1,p=l-1;while(pl<=mid&&pr<=r)t[++p]=w[pl]<w[pr]?w[pl++]:w[pr++];
	while(pl<=mid)t[++p]=w[pl++];while(pr<=r)t[++p]=w[pr++];rep(l,r,i)w[i]=t[i];
}
inline bool check(const int &k)
{
	memcpy(head,h2,(S+2)<<2);S=n*2;K=k;int lst=cgt;
	rep(1,n,i)w[i]=Nd(i,a[i]);cdq(1,n);
	bool res=Judge();cgt=lst;return res;
}
int main()
{
	n=read();int m=read();rep(1,n,i)a[i]=read();S=n*2;
	rep(1,m,i){int x=read(),y=read();ins(x,y+n);ins(x+n,y);ins(y,x+n);ins(y+n,x);}
	if(!Judge())return puts("-1"),0; memcpy(h2,head,(S+2)<<2);
	int l=0,r=1e9+10,res=-1,mid; while(l<=r)check(mid=(l+r)>>1)?r=mid-1,res=mid:l=mid+1;
	printf("%d\n",res);return 0;
}